Bài tập Toán Lớp 11 - Hàm số liên tục

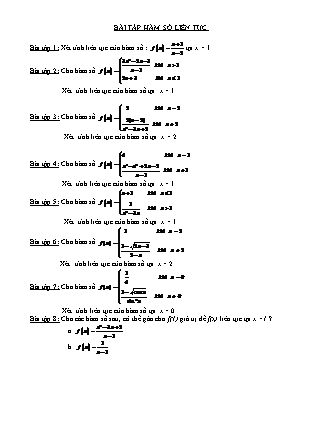
BÀI TẬP HÀM SỐ LIÊN TỤC 
Bài tập 1: Xét tính liên tục của hàm số : tại x = 1
Bài tập 2: Cho hàm số 
	 Xét tính liên tục của hàm số tại x = 1.
Bài tập 3: Cho hàm số 
	 Xét tính liên tục của hàm số tại x = 2
Bài tập 4: Cho hàm số 
 Xét tính liên tục của hàm số tại x = 1
Bài tập 5: Cho hàm số 
	 Xét tính liên tục của hàm số tại x = 1
Bài tập 6: Cho hàm số 
 Xét tính liên tục của hàm số tại x = 2
Bài tập 7: Cho hàm số 
 Xét tính liên tục của hàm số tại x = 0
Bài tập 8: Cho các hàm số sau, có thể gán cho f(1) giá trị để f(x) liên tục tại x =1 ?
	a. 
	b. 
Bài tập 9: Xác định m để f(x) liên tục tại giá trị x0 đã chỉ ra:
	a. 	x0 = 2
	b. 	x0 =1	
	c. 	x0 = 0
	d. 	x0 = 0	
	e. 	x0 = 0
Bài tập 10: Tìm điểm gián đoạn của hàm số f(x)
1. 
2. 
Bài tập 11: Hàm số f(x) liên tục trên khoảng nào ?
	1. f(x) = 3x–2x³ + x² – 3x + 2
	2. 
	3. 	
	4. 
	5. 
Bài tập12: Tìm m để hàm số sau liên tục trên .
Bài tập 13: Xét tính liên tục của hàm số f(x) trên (Biện luận theo các tham số): 
	1. 
	2. 	
	3. 
Bài tập 14: Tìm a,b để hàm số sau liên tục trên .
Bài tập 15: 
Chứng minh phương trình : x–3x = 1 có ít nhất một nghiệm thuộc ( 1 ; 2)
Chứng minh phương trình :2x+ 4x² = 3 – x có ít nhất hai nghiệm thuộc (-1; 1)
Chứng minh phương trình : x= x+ 1 có nghiệm
Chứng minh phương trình : x5 – 5x4 + 4x – 1 = 0 có 3 nghiệm trong khoảng (0;5)
Chứng minh phương trình : x³ – 3x +1 = 0 có 3 nghiệm phân biệt
Chứng minh phương trình : m( x – 1)³.( x + 2 ) + 2x + 3 = 0 luôn có nghiệm 
Chứng minh rằng: các phương trình sau luôn luôn có nghiệm:
a) cosx + m.cos2x = 0
	b) m(x – 1)3(x + 2) + 2x + 3 = 0
	c) a(x – b)(x – c) + b(x – c)(x – a) + c(x – a)(x – b) = 0
	d) (m2 + m + 1)x4 + 2x – 2 = 0
Chứng minh phương trình ax4+bx3+cx2+dx+e=0 luôn có ít nhất 2 nghiệm phân biệt với mọi a.e <0
Bài tập 16: 
Cho f(x) = ax2 + bx + c thoả mãn : 2a + 6b + 19c = 0
Chứng minh rằng phương trình ax2 + bx + c = 0 có nghiệm trong [0;]
2. Cho f(x) = ax2 + bx + c thoả mãn : 2a + 3b + 6c = 0
a) Tính a,b,c theo f(0), f(1) ,f(1/2)
b) Chứng minh rằng ba số f(0), f(1) ,f(1/2) không thể cùng dấu
c) Chứng minh rằng phương trình ax2 + bx + c = 0 có nghiệm trong (0;1)
3. Cho f(x) = ax2 + bx + c thoả mãn : = 0
a) Chứng minh rằng af() < 0 với a ¹ 0
b) Cho a > 0 , c 0
c) Chứng minh rằng phương trình ax2 + bx + c = 0 có nghiệm trong (0;1)
4. Cho hàm số f(x ) liên tục trên đoạn [a;b] thoả f(x) Î [a;b] " x Î [a;b].
 Chứng minh rằng phương trình: f(x) = x có nghiệm x Î [a;b]