Bài giảng Hình học 11 - Bài: Hai đường thẳng vuông góc

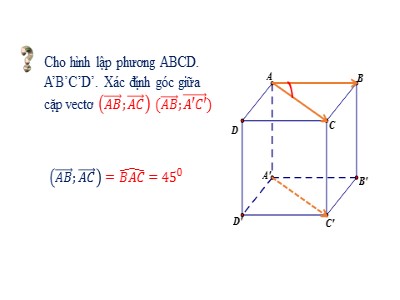
Cho hình lập phương ABCD. A’B’C’D’. Xác định góc giữa cặp vectơ 1. Góc giữa hai vectơ trong không gianABCChú ý: Góc giữa hai vectơ: 0°≤ ≤ 180°Trong không gian , cho u và v là hai vectơ khác vectơ - không. Lấy một điểm A bất kỳ, Gọi B và C là hai điểm sao cho AB = u, AC = v. Khi đó góc BAC (0°≤ BAC ≤ 180°)là góc giữa hai vectơ u và v trong không gian, ký hiệu: ( u, v )Định nghĩaI. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIANCho hình lập phương ABCD. A’B’C’D’. Xác định góc giữa cặp vectơ Nhận xét ( khi và cùng hướng ( (khi và ngược hướngCho tứ diện đều ABCD có H là trung điểm của AB. Hãy tính góc giữa các cặp vectơ sau:a) và b) và 2. Tích vô hướng của hai vectơ trong không gianĐịnh nghĩa Trong không gian cho hai vectơ và đều khác vectơ - khôngTích vô hướng của hai vectơ và là một số thực, Kí hiệu là được xác định bởi công thức:Trường hợp hoặc ta quy ước .Ví dụ 1: Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = OB = OC = 1. Gọi M là trung điểm của cạnh AB. Tính góc giữa hai vectơ Mà Vì OA, OB, OC đôi một vuông góc và OB = 1 và II. VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG1. Định nghĩa Véctơ khác vectơ – không được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ song song hoặc trùng với đường thẳng d.Cho hình lập phương ABCD. A’B’C’D’. Kể tên một số VTCP của đường thẳng d đi qua 2 điểm A, B2. Nhận xétb) Một đường thẳng d trong không gian hoàn toàn xác định nếu biết một điểm A thuộc d và một VTCP của nó.c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai VTCP cùng phương.a) Nếu là VTCP của đường thẳng d thì với k ≠ 0 cũng là VTCP của dIII. GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIANCho biết góc giữa các cặp đường thẳng sauH1H2III. GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN1. Định nghĩaGóc giữa 2 đường thẳng a và b trong không gian là góc giữa 2 đường thẳng a’ và b’ cùng đi qua 1 điểm và lần lượt song song với a và b.2. Nhận xéta) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng và vẽ một đường thẳng đi qua O và song song với đường thẳng còn lại b) Nếu là VTCP của đường thẳng a, là VTCP của đường thẳng b và thì góc giữa hai đường thẳng a và b Bằng nếu Bằng nếu Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng Ví dụ 2: Cho hình chóp S.ABC có SA = SB = SC =AB = AC = a và BC = . Tính góc giữa hai đường thẳng AB và SCTa có Và Vậy Vậy góc giữa hai đường thẳng AB và SC bằng IV. HAI ĐƯỜNG THẲNG VUÔNG GÓC1. Định nghĩaHai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900Kí hiệu: 2. Nhận xét* Nếu lần lượt là vectơ chỉ phương của 2 đường thẳng a, b thì: * Cho a // b, nếu c  a thì c  b.* Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhauHãy nêu một số phương pháp chứng minh hai đường thẳng vuông góc trong không gian? + Dùng định nghĩa. + Chứng minh tích vô hướng hai vectơ chỉ phương của hai đường thẳng đó bằng 0.+Ví dụ 3: Cho tứ diện ABCD có AB  AC và AB  BD. Gọi P và Q lần lượt là trung điểm AB và CD. Chứng minh rằng AB PQTa có Và Có Vậy . Vậy AB PQHãy lấy ví dụ cụ thể về hai đường thẳng vuông góc (cắt nhau, không cắt nhau) trong thực tế? * Hai đường thẳng vuông góc (cắt nhau) Xà ngang và cột dọc của một khung thành* Hai đường thẳng vuông góc (chéo nhau) Tuyến đường sắt trên cao và tuyến đường bộ bên dưới cho ta hình ảnh của hai đường thẳng vuông góc Qua bài học em cần nắmGÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIANVECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNGTÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIANHAI ĐƯỜNG THẲNG VUÔNG GÓCGÓC GIỮA HAI VECTƠ TRONG KHÔNG GIANBÀI TẬP TRẮC NGHIỆM KHÁCH QUANCâu 1: Cho α là góc giữa và trong không gian. Khẳng định nào đúng? α là một góc nhọn B. α không thể là một góc tù C. α có thể là một góc tù D. α là một góc vuôngCâu 2: Trong không gian vectơ chỉ phương của đường thẳng: A. Vuông góc với đường thẳng đóB. Có giá song song với đường thẳng đó C. Có giá song song hoặc trùng với đường thẳng đóD. Có giá vuông góc với đường thẳng đóCâu 3: Trong không gian cho ba đường thẳng phân biệt a , b , c. Mệnh đề nào sau đây đúng? Nếu a và b cùng vuông góc với c thì a / / b. Nếu a / / b, c ⊥ a thì c ⊥ b Nếu góc giữa a và c bằng góc giữa b và c thì a / / b.Nếu a và b cùng nằm trong mặt phẳng () và c / /() thì góc giữa a và c bằng góc giữa b và c CHÂN THÀNH CẢM ƠN!