Giáo án Đại số Lớp 11 - Chương 1: Hàm số lượng giác và phương trình lượng giác - Bài 1: Hàm số lượng giác - Năm học 2021-2022 - Trường THPT Hoa Sen

CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC 
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
(24 tiết)
x.1: HÀM SỐ LƯỢNG GIÁC
PHẦN I: TÓM TẮT LÝ THUYẾT
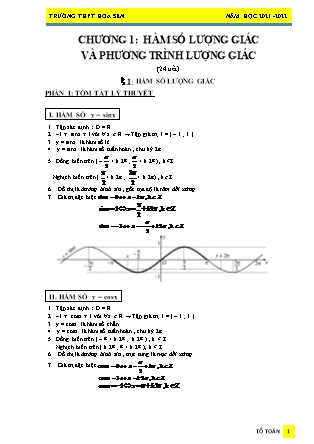
I. HÀM SỐ y = sinx 
 1. Tập xác định : D = R 
 2. –1 £ sinx £ 1 với "x Î R Þ Tập giá trị I = [ – 1 ; 1 ] 
 3. y = sinx là hàm số lẻ
 4. y = sinx là hàm số tuần hoàn , chu kỳ 2p 
 5. Đồng biến trên ( – + k.2p ; + k.2p) , kÎZ 
 Nghịch biến trên (+ k.2p ; + k.2p) , kÎZ 
Đồ thị là đường hình sin , gốc tọa độ là tâm đối xứng . 
Giá trị đặc biệt 
II. HÀM SỐ y = cosx 
 1. Tập xác định : D = R 
 2. –1 £ cosx £ 1 với "x Î R Þ Tập giá trị I = [ – 1 ; 1 ] 
 3. y = cosx là hàm số chẵn
 4. y = cosx là hàm số tuần hoàn , chu kỳ 2p 
 5. Đồng biến trên ( – p + k.2p ; k.2p ) , k Î Z .
 Nghịch biến trên ( k.2p ; p + k.2p ), k Î Z .
Đồ thị là đường hình sin , trục tung là trục đối xứng . 
Giá trị đặc biệt 
III. HÀM SỐ y = tanx 
 1. Tập xác định : D = R\ { + k.p , k Î Z } và – ¥ < tanx < +¥ với "x Î D . 
 2. Tập giá trị I = R 
 3. y = tanx là hàm số lẻ , 
 4. y = tanx là hàm số tuần hoàn , chu kỳ p 
 5. Đồng biến trên ( – + k.p ; + k.p ) , k Î Z .
 6. Đồ thị nhận gốc tọa độ là tâm đối xứng .
 7. Giá trị đặc biệt 
IV. HÀM SỐ y = cotx 
 1. Tập xác định : D = R\ { k.p } và – ¥ < cotx < + ¥ với "x Î D . 
 2. Tập giá trị I = R . 
 3. y = cotx là hàm số lẻ .
 4. y = cotx là hàm số tuần hoàn , chu kỳ p 
 5. Nghịch biến trên ( k.p ; p+ k.p ) , k Î Z .
 6. Đồ thị nhận gốc tọa độ là tâm đối xứng 
7. Giá trị đặc biệt 
CHÚ Ý : 1) ·
 · 
 · 
· 
 · 
 · 
 3) · 
 ·
 · 
 4) · 
 · 
 · 
BẢNG TÓM TẮT CÁC HÀM SỐ LƯỢNG GIÁC
Hàm số
Giá trị đặc biệt
Tập xác định
Tập giá trị
Tính chẵn lẻ
Đồ thị
 y=sinx
sinx = 0x = k
sinx = 1 x = 
sinx = –1x = –
 R
[ – 1 ; 1 ]
 Lẻ
Đường hình sin
Tâm đối xứng là gốc tọa độ
y=cosx
cosx = 0x = 
cosx = 1 x = 
cosx = –1x = 
 R
[ – 1 ; 1 ]
 Chẵn
Đường hình sin
Trục đối xứng là trục tung
y=tanx
tanx = 0 x = k
tanx = 1 x = 
tanx = –1x = –
R\
R
 Lẻ
Luôn đồng biến
Tâm đối xứng là gốc tọa độ
y=cotx
cotx = 0 x = 
cotx = 1 x = 
cotx = –1x = –
R\
R
 Lẻ
Luôn đồng biến
Tâm đối xứng là gốc tọa độ
PHẦN II: BÀI TẬP CƠ BẢN
Bài 1 : Xác đinh giá trị của x trên đoạn [ – ] để hàm số y = 
 a) Nhận giá trị bằng 0 . b) Nhận giá trị bằng – 1 
 c) Nhận giá trị dương. d) Nhận giá trị âm.
Bài 2 : Xác đinh giá trị của x trên đoạn [ – ] để hàm số y = 
 a) Nhận giá trị bằng 1 . b) Nhận giá trị bằng – 1 
 c) Nhận giá trị dương. d) Nhận giá trị âm.
Bài 3 : Tìm TXĐ của các hàm số sau :
 1) y = 2) y = 
 3) y = 4) y = 
 5) y = 6) y = 
 7) y = tan (2x +) 8) y = cot( x –) 
 9) y = 10) y = tan 
Bài 4 : Tìm GTLN , GTNN của các hàm số sau :
 1) y = 3 – 2sinx 2) y = 2 + 1 
 3) y = sinx + cosx + 3 4) y = 5 + sinx + cosx 
 5) y = 2sin(x – ) – 1 6) y = 
x.2 PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
PHẦN 1: TÓM TẮT LÝ THUYẾT
I. PHƯƠNG TRÌNH: sinu = a , u = x hoặc u = f(x)
 1. Điều kiện có nghiệm 
 · Nếu £ 1 : Phương trình có nghiệm
 · Nếu > 1 : Phương trình vô nghiệm
 2. Công thức nghiệm tính theo rad : ( Trong trường hợp có nghiệm )
 · TH 1 : a là sin của góc đặc biệt a : sina = a 
 Phương trình sinu = a Û sinu = sina Û ( )
 · TH 2 : a không phải là sin của góc đặc biệt , 
 Phương trình sinu = a Û ()
 3. Công thức nghiệm tính theo độ : 
 · Nếu a = sinb0 Û () 
 4. Phương trình sinu = sinv : 
 · sinu = sinv Û () 
 5. CHÚ Ý : 1) Nếu u = f(x) ta phải giải tìm x mới được nghiệm của phương trình . 
 2) Không dùng ký hiệu arcsin trong trường hợp nghiệm tính theo độ .
 3) – sinu = sin(– u ) ; cosu = sin( – u ) 
 6. Công thức nghiệm của một số phương trình đặc biệt 
 1) sinu = 1 Û u = + k.2p () 
 2) sinu = 0 Û u = k.p ( 
 3) sinu = – 1 Û u = + k.2p ( ) 
II. PHƯƠNG TRÌNH cosu = a , u = x hoặc u = f(x)
 1. Điều kiện có nghiệm 
 · Nếu £ 1 : Phương trình có nghiệm
 · Nếu > 1 : Phương trình vô nghiệm
 2. Công thức nghiệm tính theo rad : ( Trong trường hợp có nghiệm )
 · TH 1 : a là cos của góc đặc biệt a : cosa = a 
 Phương trình cosu = a Û cosu = cosa Û ( )
 · TH 2 : a không phải là cos của góc đặc biệt , 
 Phương trình cosu = a Û ( )
 3. Công thức nghiệm tính theo độ : 
 · Nếu a = cosb0 Û ( ) 
 4. Phương trình cosu = cosv : 
 · cosu = cosv Û ( ) 
 5. CHÚ Ý : 1) Nếu u = f(x) ta phải giải tìm x mới được nghiệm của phương trình . 
 2) Không dùng ký hiệu arccos trong trường hợp nghiệm tính theo độ .
 3) – cosu = cos(p – u ) ; sinu = cos( – u ) 
 6. Công thức nghiệm của một số phương trình đặc biệt 
 1) cosu = 1 Û u = k.2p ( ) 
 2) cos u = 0 Û u = + k.p ( )
 3) cosu = – 1 Û u = p + k.2p ( ) 
III. PHƯƠNG TRÌNH tanu = a , u = x hoặc u = f(x)
 1. Điều kiện có nghiệm 
 Với mọi a Î R phương trình luôn có nghiệm
 2. Công thức nghiệm tính theo rad : 
 · TH 1 : a là tan của góc đặc biệt a : tana = a 
 Phương trình tanu = a Û tanu = tana Û u = a + k.p ( )
 · TH 2 : a không phải là tan của góc đặc biệt , 
 Phương trình tanu = a Û u = arctana + k.p ( )
 3. Công thức nghiệm tính theo độ : 
 · Nếu a = tanb0 Û u = b0 + k.1800 ( ) 
 4. Phương trình tanu = tanv : 
 · tanu = tanv Û u = v + k.p ( ) 
 5. CHÚ Ý : 1) Nếu u = f(x) ta phải giải tìm x mới được nghiệm của phương trình . 
 2) Không dùng ký hiệu arctan trong trường hợp nghiệm tính theo độ .
 3) – tanu = tan(– u ) ; cotu = tan( – u ) 
 6. Công thức nghiệm của một số phương trình đặc biệt 
 1. tanu = 1 Û u = + k.p ( ) 
 2. tanu = 0 Û u = k.p ( )
 3. tanu = –1 Û u = – + k.p ( ) 
IV. PHƯƠNG TRÌNH cotu = a , u = x hoặc u = f(x)
 1. Điều kiện có nghiệm 
 Với mọi a Î R phương trình luôn có nghiệm
 2. Công thức nghiệm tính theo rad : 
 · TH 1 : a là cotan của góc đặc biệt a : cota = a 
 Phương trình cotu = a Û cotu = cota Û u = a + k.p ( )
 · TH 2 : a không phải là cotan của góc đặc biệt , 
 Phương trình cotu = a Û u = arctcot + k.p ( )
 3. Công thức nghiệm tính theo độ : 
 · Nếu a = cotb0 Û u = b0 + k.1800 ( ) 
 4. Phương trình cotu = cotv : 
 · cotu = cotv Û u = v + k.p ( ) 
 5. CHÚ Ý : 1) Nếu u = f(x) ta phải giải tìm x mới được nghiệm của phương trình . 
 2) Không dùng ký hiệu arccot trong trường hợp nghiệm tính theo độ .
 3) – cotu = cot(– u ) ; tanu = cot( – u ) 
 6. Công thức nghiệm của một số phương trình đặc biệt 
 1) cotu = 1 Û u = + k.p ( ) 
 2) cotu = 0 Û u = + k.p ( )
 3) cotu = –1 Û u = – + k.p ( ) 
Sơ đồ tư duy:
PHẦN 2: BÀI TẬP CƠ BẢN 
Bài 1 : Giải các phương trình :
 1) sin ( x + ) = 2) sin ( 2x – ) = –
 3) 4) sin2x = -1
 5) sin ( x + ) = 6) sin3x = 
 7) sin2x = 8) sin(– ) = – 
 9) sin(2x + 300) = 10) 
 11) sin2x = sin( x – ) 12) sin3x + sinx = 0 
 13) sin2x = cosx. 14) sin2x = 1/4 
Bài 2: Giải các phương trình :
 1) cos( x – ) = 2) cos( 2x + ) = –
 3) 4) 
 5) 6) 
 7) cos ( 2x – ) = 1 8) cos5x = 
 9) cos2x = 10) cos(+ ) = – 
 11) cos(2x – 300) = – 12) cos(– 2x) = 
 13) 14) | cos ( 2x – 1 ) | = 1 
 Bài 3 : Giải các phương trình :
 9) tan( 2x – ) = 10) tan( 5x + ) = 
 11) tan2x = cotx 12) tan ( 2x – 400 ) = -1 
 13) | tan( x + ) | = 1 14) tan5x = cotx 
Bài 4: Giải phương trình sau
 9) 10) cot( 3x + 5 ) = 4
 11) 12) 
x.3 PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
PHẦN 1: TÓM TẮT LÝ THUYẾT
I. PHƯƠNG TRÌNH BẬC NHẤT MỘT HÀM SỐ LƯỢNG GIÁC
1. Phương trình a.sinu + b = 0 hoặc a.cosu + b = 0 a ¹ 0 , u = x hoặc u = f(x)
Cách giải : Đưa về phương trình cơ bản sinu = – hoặc cosu = – 
 a. Nếu £ 1 : Phương trình có nghiệm
 b. Nếu > 1 : Phương trình vô nghiệm
2. Phương trình a.tanu + b = 0 hoặc a.cotu + b = 0 , a ¹ 0 , u = x hoặc u = f(x)
Cách giải : Đưa về phương trình cơ bản tanu = – hoặc cotu = – 
 Phương trình luôn có nghiệm
II. PHƯƠNG TRÌNH BẬC HAI MỘT HÀM SỐ LƯỢNG GIÁC 
1. Phương trình a.sin2u+ bsinu + c = 0 ( 1 ) hoặc a.cos2u+ bcosu + c = 0 (1)
 với a ¹ 0 , u = x hoặc u = f(x)
Cách giải : 
 · Đặt ẩn phụ sinu = t (hoặc cosu = t ), với – 1 £ t £ 1 ( hay | t | £ 1 ) 
 · ( 1 ) Û at2 + bt + c = 0 ( 2 )
 · Giải phương trình ( 2 ) : nhận nghiệm thỏa mãn điều kiện , loại nghiệm không thỏa mãn
 · Giải phương trình cơ bản sinu = t (hoặc cosu = t) với từng giá trị t , ta được nghiệm phương trình đã cho. 
2. Phương trình a.tan2u+ btanu + c = 0 ( 1 ) hoặc a.cot2u+ bcotu + c = 0 ( 1 ) 
 với a ¹ 0 , u = x hoặc u = f(x)
Cách giải : 
 · Điều kiện : u ¹ + kp (hoặc u ¹ )
 · Đặt ẩn phụ tanu = t (hoặc cotu = t) với tÎ R 
 · ( 1 ) Û at2 + bt + c = 0 ( 2 )
 · Giải phương trình ( 2 ) : nhận mọi nghiệm t tìm được 
 · Giải phương trình cơ bản tanu = t (hoặc cotu = t) với từng giá trị t, ta được nghiệm phương trình đã cho . 
III. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI sinu , cosu 
1. Công thức biến đổi biểu thức asinu + bcosu 
 ( 1 )
 Dựa vào các công thức cộng :
 · sinacosb ± cosasinb = sin( a ± b )
 · cosacosb ± sinasinb = cos( a – b )
 · cosacosb – sinasinb = cos( a + b )
 đưa biểu thức ( 1 ) về một trong các dạng thích hợp sau : 
 · 
 · 
 · 
 · 
2. Phương trình dạng asinu + bcosu = c ( a2 + b2 ¹ 0 ) ( 2 )
 a. Nếu a = 0 , b ¹ 0 hoặc a ¹ 0 , b = 0 : Đưa p.trình ( 2 ) về dạng cơ bản 
Nếu a ¹ 0 và b ¹ 0 , áp dụng công thức biến đổi vế trái đưa p.trình ( 2 ) về một trong các dạng cơ bản sau :
 · hoặc 
 CHÚ Ý : 1. Phương trình có nghiệm Û a2 + b2 ³ c2
sinx + cosx = cos ( x – ) 
sinx – cosx = cos ( x + ) 
PHẦN 2: BÀI TẬP CƠ BẢN 
Bài 1 : Giải các phương trình sau :
 1) 3sin2x – = 0 2) 3cosx + 5 = 0 
 3) 2cosx + = 0 4) 3sin2x – = 0 
 5) 3cosx + 5 = 0 6) 2sinx – = 0 
 7) 2sinx + 1 = 0 8) 3sin4x – 2 = 0
 9) 2sin2x – 5 = 0 10) 2cosx + = 0 
 11) 2cos(3x + 300) – 1 = 0 12) 2cos( –) + = 0 
 13) 3tanx – = 0 14) cot2x + = 0 
 15) tan (x + 300) – = 0 16) cot(2x – ) + 1 = 0 
 17) 3tanx + = 0 18) 3cot( x + 300 ) + = 0 
Bài 2 : Giải các phương trình sau :
 1) 2cos2x + 5cosx + 2 = 0 2) 2sin2x – 3sinx + 1 = 0 
 3) 9sin22x – 6sin2x + 1 = 0 4) 3cos23x + 2cos3x + 2 = 0
 5) 2sin2x – 5sinx + 2 = 0 6) 2sin2x – 3sinx + 1 = 0 
 7) 9sin22x – 6sin2x + 1 = 0 8) 6sin23x – 5sin3x + 1 = 0 
 9) 10cos2x – 3cosx – 1 = 0 10) 2cos25x – 3cos5x + 1 = 0 
 Bài 3 : Giải các phương trình sau :
 1) tan22x – 4tan2x + 3 = 0 2) 2cot2x + cotx – 1 = 0
 3) 3tan2 – 10tan + 3 = 0 4) tan2x – (1 + )tanx + = 0
 5) tan22x – 4tan2x + 3 = 0 6) 2tan2x – 5tanx – 3 = 0
 7) cot23x + 3cot3x + 2 = 0 8) 2cot2x + cotx – 1 = 0
 9) cot2 – 4cot + 3 = 0 10) 3cot22x + 2cot2x – 8 = 0
Bài 4 : Giải các phương trình sau : 
sin2x – cos2x = 1 
12sinx + 5cosx – 13 = 0 
2( sin3x + cos3x ) = 
sinx – cosx = 
 5) cos3x –sin3x + = 0
sin4x + cos4x + = 0 
PHẦN 4: CÁC DẠNG TOÁN THƯỜNG GẶP
I. Phương trình thuần nhất bậc hai đối với sinu , cosu : 
 a.sin2u + b.sinucosu + c.cos2u = d ( 1 )
 Xét hai trường hợp :
 * TH 1 : cosu = 0 Û sin2u = 1 thế vào phương trình 
 + Thỏa mãn : Giá trị x làm cosu = 0 là nghiệm phương trình 
 + Không thỏa mãn : Giá trị x làm cosu = 0 không phải là nghiệm phương trình 
hgnnbes * TH 2 : cosu ¹ 0 : chia hai vế phương trình cho cos2u , đưa phương trình về dạng
 a.tan2u+ b.tanu + c = 0 ( 2 )
 CHÚ Ý : = 1 + tan2u 
Bài 1: Giải các phương trình sau : 
 1) 2sin2x – sinx.cosx – 3cos2x = 0 2) sin2+ 2sincos – 2cos2 = 
 3) 2cos2x – 6sinx.cosx – 4 sin2x = – 4 4) 2sin2x + 5sinxcosx – cos2x = 3
 5) 2cos22x – 6sin2x.cos2x + sin22x = 1 6) 3cos2x – 4sinx.cosx + sin2x = 1
 7) 3sin2x – 4sinx.cosx + 5cos2x = 2 8) 2sin2x – 5sinxcosx – cos2x = – 2 
II. PHƯƠNG TRÌNH ĐƯA VÀ DẠNG BẬC 1, BẬC 2 CỦA MỘT HÀM SỐ LƯỢNG GIÁC
Bài 2: Giải các phương trình sau : 
 1) 2cos2x – sinx + 1 = 0 2) cos4x + 3sin2x – 2 = 0 
 3) cos2x – 5sinx – 3 = 0 4) cos2x + 3sinx + 1 = 0
 5) 2cos6x + 3sin3x + 3sin23x + 2 = 0 6) 2cos2x + 5cosx – 2cos2x – 3 = 0 
 Bài 3: Giải các phương trình sau : 
 1) 2sin2x + 5cosx – 5 = 0 2) 6sin23x + 5cos3x – 7 = 0
 3) 3sin22x + 7cos2x – 3 = 0 4) 2sin23x+ 5cos3x + 1 = 0
 5) 2sin2x + 3cosx + cos2x – 3 = 0 6) sin2x – cosx – cos2x – 1 = 0
Bài 4 : Giải các phương trình sau : 
 1) 6cos2x – sinx – 5 = 0 2) 8cos22x + 2sin2x – 7 = 0 
 3) 3cos2x – 2sinx + 2 = 0 4) cos23x – 2sin3x + 2 = 0
 Bài 5 : Giải các phương trình sau : 
 1) tanx – 2cotx – 1 = 0 2) cot2x + 3tan2x – 4 = 0
 3) 2cot3x – 5tan3x – 3 = 0 4) 5tanx – 2cotx – 3 = 0
Bài 6 : Giải các phương trình sau : 
 1) 3tan2x – + tanx = 0 2) 4tan2x – = 0 
 3) tan2 + + tan – 4 = 0 4) tan3x – + 5 = 0 
 5) 2cot2x + 2cotx + – 4 = 0 6) + 3cot2x – 7 = 0 
PHẦN 5: BÀI TẬP TỰ LUYỆN 
Bài 1 : Giải các phương trình sau :
 1) sinx – cosx = 2sin3x 2) cos5x – sin3x = ( cos5x – sin7x ) 
 3) sin – cos = sin2x 4) sin4x – sin5x = cos4x + cos5x 
 5) ( sinx – cosx )2 + cos2x = cosx + 1 6) 8( sin6x + cos6x ) = 4 – 3sin4x 
Bài 2 : Giải các phương trình sau : 
 1) 2sin2x – 5sinx + 2 = 0 2) cos2 + cos – 2 = 0 
 3) tan2x – (1 + )tanx + = 0 4) cot2 – 4cot + 3 = 0 
 5) cos2x + 2cosx = 2sin2 6) sin2x – cosx – cos2 – 1 = 0 
 7) 3sin2x – 2sin2x + 5cos2x = 2 8) 2sin2x – 5sinxcosx – cos2x = – 2 
 9) cos3x –sin3x + = 0 10) sin4x + cos4x + = 0 
 11) sin – cos = sin2x