Giáo án Đại số Lớp 11 - Chủ đề 1, Bài 3: Một số phương trình lượng giác thường gặp

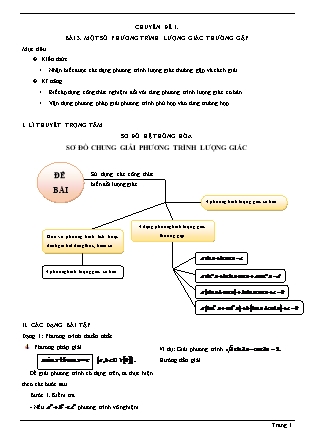
CHUYÊN ĐỀ 1.
BÀI 3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
Mục tiêu
Kiến thức
Nhận biết được các dạng phương trình lượng giác thường gặp và cách giải.
Kĩ năng
Biết áp dụng công thức nghiệm đối với từng phương trình lượng giác cơ bản.
Vận dụng phương pháp giải phương trình phù hợp vào từng trường hợp. 
I. LÍ THUYẾT TRỌNG TÂM
SƠ ĐỒ HỆ THỐNG HÓA
SƠ ĐỒ CHUNG GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC 
4 dạng phương trình lượng giác 
thường gặp
Đưa về phương trình tích hoặc đánh giá bất đẳng thức, hàm số
4 phương trình lượng giác cơ bản
ĐỀ BÀI
4 phương trình lượng giác cơ bản 
Sử dụng các công thức biến đổi lượng giác
II. CÁC DẠNG BÀI TẬP
Dạng 1: Phương trình thuần nhất
Phương pháp giải
Để giải phương trình có dạng trên, ta thực hiện theo các bước sau
Bước 1. Kiểm tra
- Nếu phương trình vô nghiệm.
- Nếu khi đó phương trình có nghiệm, ta thực hiện tiếp Bước 2.
Bước 2. Chia hai vế phương trình cho ta được 
 Đặt phương trình (**) trở thành
Phương trình là phương trình lượng giác dạng cơ bản nên dễ dàng giải được.
Một số dạng mở rộng:
với
Dạng đặc biệt:
Ví dụ: Giải phương trình 
Hướng dẫn giải
Ta có 
Vậy phương trình đã cho có nghiệm 
Xin giới thiệu quý thầy cô Bộ File Word tài liệu Dạy thêm theo chuyên đề 
1. Toán Lớp 10 – 11 – 12: Đầy đủ các chuyên đề Đại số & Hình học + Bộ đề kiểm tra 15 phút, 1 tiết, thi Học kỳ có lời giải và đáp án đầy đủ. 
2. Bộ đề Ôn thi THPT QG gần 200 đề của các thầy cô và trung tâm Luyện thi trên cả nước có đáp án và giải Chi tiết.
Quý thầy cô nào cần xin Liên hệ Số điện thoại Hoặc Zalo: 0911.465.929
Xin cám ơn!
Ví dụ mẫu
Ví dụ 1. Giải phương trình 
Hướng dẫn giải
Ta có 
Xét phương trình có nên vô nghiệm.
Vậy phương trình có nghiệm 
Ví dụ 2. Giải phương trình 
Hướng dẫn giải 
Ta có 
Vậy phương trình có nghiệm 
Bài tập tự luyện dạng 1
Câu 1: Phương trình có nghiệm là
A. 	B. 	
C. 	D. 
Câu 2: Phương trình có nghiệm âm lớn nhất bằng
A. 	B. 	C. 	D. 
Câu 3: Nghiệm của phương trình là
A. 	B. 	
C. 	D. 
Câu 4: Số nghiệm của phương trình trên khoảng là
A. 0.	B. 1.	C. 2.	D. 3.
Câu 5: Điều kiện để phương trình vô nghiệm là 
A. 	B. 	C. 	D. 
Câu 6: Điều kiện để phương trình có nghiệm là
A. 	B. 	C. 	D. 
Câu 7: Phương trình tương đương với phương trình nào sau đây?
A. 	B. 	
C. 	D. 
Câu 8: Trong các phương trình sau phương trình nào có nghiệm?
A. 	B. 	
C. 	D. 
Câu 9: Cho phương trình trên đoạn . Chọn câu trả lời đúng.
A. Phương trình có nghiệm 	B. Phương trình có nghiệm 
C. Phương trình có nghiệm 	D. Phương trình có nghiệm 
Câu 10: Phương trình có nghiệm là
A. 	B. 	
C. 	D. 
Câu 11: Phương trình nào sau đây vô nghiệm?
A. 	B. 	
C. 	D. 
Câu 12: Số nghiệm của phương trình thuộc đoạn là
A. 3.	B. 4.	C. 5.	D. 2.
Câu 13: Phương trình có các họ nghiệm là
A. 	B. 	
C. 	D. 
Câu 14: Phương trình có nghiệm dương nhỏ nhất bằng
A. 	B. 	C. 	D. 0.
Câu 15: Phương trình có nghiệm dương nhỏ nhất bằng
A. 	B. 	C. 	D. 0.
Câu 16: Nghiệm của phương trình với là
A. 	B. 	C. 	D. 
Câu 17: Để phương trình có nghiệm thì giá trị của m là
A. 	B. 	
C. 	D. 
Câu 18: Phương trình có số họ nghiệm là
A. 1.	B. 3.	C. 2.	D. 0.
Câu 19: Phương trình có các họ nghiệm là
A. 	B. 	
C. 	D. 
Câu 20: Cho phương trình Với thì nghiệm của phương trình là
A. 	B. 	C. 	D. 
Dạng 2:Phương trình bậc hai của một hàm số lượng giác
Phương pháp giải
Phương trình bậc hai đối với một hàm số lượng giác có dạng tổng quát 
Trong đó:
t là một trong các hàm số và 
Khi đặt ẩn phụ để giải ta phải lưu ý đến điều kiện của ẩn phụ. Nếu đặt
+) thì điều kiện 
+) thì điều kiện 
+) thì điều kiện 
Khi tìm được thỏa mãn thì phải giải tiếp 
Ví dụ: Giải phương trình 
Hướng dẫn giải
Đặt điều kiện 
Phương trình đã cho trở thành
Kết hợp với điều kiện ta được 
Với thì 
Vậy phương trình đã cho có nghiệm 
Ví dụ mẫu
Ví dụ. Giải phương trình 
Hướng dẫn giải
Ta có 
Trường hợp 1: 
Trường hợp 2: (loại).
Vậy phương trình đã cho có nghiệm 
Bài tập tự luyện dạng 2
Câu 1: Phương trình có nghiệm là
A. 	B. 	
C. 	D. 
Câu 2: Với , phương trình có nghiệm là
A. 	B. 	C. 	D. Vô nghiệm.
Câu 3: Nghiệm dương bé nhất của phương trình là
A. 	B. 	C. 	D. 
Câu 4: Xét phương trình trên đoạn Chọn câu trả lời đúng.
A. Phương trình có 3 nghiệm.	B. Phương trình có 4 nghiệm.
C. Phương trình có 2 nghiệm. 	D. Phương trình vô nghiệm.
Câu 5: Nghiệm của phương trình thỏa mãn điều kiện là 
A. 	B. 	C. 	D. 
Câu 6: Nghiệm của phương trình là
A. 	B. 	C. 	D. 
Câu 7: Với phương trình có nghiệm là
A. 	B. 	C. 	D. 
Câu 8: Với phương trình có nghiệm là
A. 	B. 	C. 	D. 
Câu 9: Nghiệm của phương trình là 
A. 	B. 	
C. 	D. 
Câu 10: Nghiệm âm lớn nhất của phương trình là
A. 	B. 	C. 	D. 
Câu 11: Trong các phương trình sau phương trình nào có nghiệm?
A. 	B. 	
C. 	D. 
Câu 12: Xét phương trình trên đoạn Lựa chọn phương án đúng.
A. Phương trình có 2 nghiệm.	B. Phương trình có 4 nghiệm. 	
C. Phương trình vô nghiệm. 	D. Cả A, B, C đều sai.
Câu 13: Phương trình có nghiệm là
A. 	B. 	
C. 	D. 
Câu 14: Xét phương trình trên đoạn Chọn câu trả lời đúng?
A. Phương trình có 5 nghiệm.	B. Phương trình có 4 nghiệm.
C. Phương trình có 6 nghiệm.	D. Phương trình có 3 nghiệm.
Câu 15: Xét phương trình trên đoạn Chọn câu trả lời đúng?
A. Phương trình có 2 nghiệm.	B. Phương trình có 4 nghiệm.
C. Cả A, B, D đều sai.	D. Phương trình có 3 nghiệm.
Câu 16: Cho x thỏa mãn phương trình sau 
Giá trị của biểu thức là
A. 0.	B. 2.	C. 3.	D. 
Câu 17: Cho x thỏa mãn phương trình Giá trị của biểu thức là
A. 1.	B. 0,5.	C. 	D. 0.
Câu 18: Cho là nghiệm của một trong phương trình sau, hỏi đó là phương trình nào?
A. 	B. 	
C. 	D. 
Câu 19: Cho phương trình Nếu giải phương trình bằng cách đặt thì phương trình trên sẽ tương đương với phương trình nào dưới đây?
A. 	B. 	
C. 	D. 
Câu 20: Cho phương trình Nếu giải phương trình bằng cách bình phương hai vế thì ta được phương trình nào sau đây?
A.	B. 	
C.	D. 
Dạng 3. Phương trình lượng giác đẳng cấp
Phương pháp giải
Phương trình lượng giác đẳng cấp có dạng tổng quát
Ta có thể giải phương trình lượng giác đẳng cấp theo hai cách sau
Cách 1:
Bước 1. Kiểm tra có là nghiệm của phương trình hay không, nếu có thì nhận nghiệm này. 
Bước 2. Nếu thì chia cả hai vế của phương trình cho đưa về phương trình bậc hai theo .
Bước 3. Đặt đưa về phương trình bậc hai để giải.
Cách 2: Dùng công thức hạ bậc.
Đưa phương trình đã cho về phương trình
Đây là phương trình bậc nhất đối với sin và cosin ta đã biết cách giải ở dạng 1.
Tổng quát: Đối với phương trình đẳng cấp bậc trong đó ta cũng giải tương tự theo hai cách.
Cách 1: Nếu thì chia cả hai vế cho .
Cách 2: Dùng công thức hạ bậc.
Ví dụ: Giải phương trình sau
Hướng dẫn giải
Với 
Thay vào phương trình (1) ta có 
phương trình vô nghiệm.
Với . Chia cả hai vế của phương trình (1) cho ta được
Đặt phương trình (2) trở thành
Vậy phương trình đã cho có nghiệm
Ta có 
Vậy phương trình có 2 họ nghiệm là
Ví dụ mẫu
Ví dụ. Cho phương trình Tìm m để phương trình có nghiệm.
Hướng dẫn giải
	- Nếu Phương trình có dạng 
Để phương trình có nghiệm thì 
	- Nếu thì ta chia cả hai vế của phương trình cho .
Phương trình đã cho trở thành 
Với thì phương trình (1) là phương trình bậc hai ẩn 
Xét 
Để phương trình đã cho có nghiệm thì 
Kết hợp (*) và (**), ta được là những giá trị cần tìm.
Vậy với thì phương trình đã cho có nghiệm.
Bài tập tự luyện dạng 3
Câu 1: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. 
Câu 2: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. 
Câu 3: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. 
Câu 4: Cho x thỏa mãn phương trình . Giá trị nguyên của là
	A. 1.	B. 	C. 3.	D. 2.
Câu 5: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. 
Câu 6: Giải phương trình ta được nghiệm là
	A. 	B. 	
	C. 	D. 
Câu 7: Cho x thỏa mãn phương trình Giá trị nguyên của là
	A. 1.	B. 	C. 	D. 
Câu 8: Phương trình có thể được đưa về phương trình nào trong các phương trình sau
	A. 	B. 	
	C. 	D. Một phương trình khác. 
Câu 9: Kết quả nào cho dưới đây là đúng? Phương trình có tập nghiệm là
	A. 	B. 	
	C. 	D. Đáp án khác.
Câu 10: Khi thì phương trình 
 có bao nhiêu họ nghiệm?
	A. 0.	B. 2.	C. 1.	D. 3.
Câu 11: Cho phương trình Nghiệm của phương trình là
	A. 	B. 	
	C. 	D. 
Câu 12: Phương trình có tập nghiệm là
	A. 	B. 	
	C. Phương trình vô số nghiệm. 	D. Đáp án khác.
Câu 13: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. 
Câu 14: Phương trình có tập nghiệm là
	A. 	B. 	
	C. Phương trình vô số nghiệm.	D. Đáp án khác.
Câu 15: Cho x thỏa mãn phương trình Giá trị của biểu thức 
 là
	A. 1.	B. 0.	C. 3.	D. 2.
Câu 16: Cho phương trình Số nghiệm của phương trình đã cho trong khoảng là 
	A. 2.	B. 3.	C. 0.	D. 1.
Câu 17: Cho phương trình khẳng định đúng là
	A. Phương trình có 1 họ nghiệm.	B. Phương trình vô nghiệm.	
	C. Phương trình có 2 họ nghiệm.	D. Cả A, B, C đều sai.
Câu 18: Cho x thỏa mãn phương trình Giá trị của biểu thức là
	A. 1.	B. 	C. 3.	D. 2.
Câu 19: Cho phương trình khẳng định đúng là
	A. Phương trình có 2 họ nghiệm.	B. Phương trình vô nghiệm.
	C. Phương trình có 1 họ nghiệm. 	D. Cả A, B, C đều sai.
Câu 20: Cho phương trình Giá trị của m để phương trình có nghiệm là
	A. 	B. 	C. 	D. 
Dạng 4. Phương trình lượng giác đối xứng
Phương pháp giải
Phương trình lượng giác đối xứng có dạng tổng quát
Trong đó 
Để giải phương trình lượng giác đối xứng, ta làm như sau.
Đặt 
Điều kiện 
Ta có 
Khi đó phương trình đã cho trở thành
Đây là phương trình bậc hai đã biết cách giải.
Chú ý: Cách giải trên áp dụng cho phương trình
Đặt 
Ví dụ.
Hướng dẫn giải
Đặt 
Khi đó phương trình (1) trở thành
Kết hợp với điều kiện ta được
Vậy phương trình có 2 họ nghiệm là
Ví dụ mẫu
Ví dụ 1. Giải phương trình 
Hướng dẫn giải
Đặt 
Khi đó phương trình (1) trở thành 
- Nếu thì 
- Nếu thì 
Vậy phương trình đã cho có 4 họ nghiệm 
Ví dụ 2. Giải phương trình 
Hướng dẫn giải
Đặt 
Khi đó phương trình (*) trở thành 
Suy ra 
Vậy phương trình đã cho có 2 họ nghiệm 
Bài tập tự luyện dạng 4
Câu 1: Cho phương trình. Đặt ta được phương trình nào dưới đây?
	A. 	B. 	C. 	D. 
Câu 2: Nếu thì nhận giá trị là
	A. 	B. 1.	C. 	D. 
Câu 3: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. Vô nghiệm.
Câu 4: Cho phương trình Nghiệm dương nhỏ nhất của phương trình là
	A. 	B. 	C. 	D. 
Câu 5: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. Vô nghiệm.
Câu 6: Cho phương trình Nếu thì giá trị của t thỏa mãn là
	A. 	B. 	C. 	D. 
Câu 7: Cho phương trình Số nghiệm của phương trình thỏa mãn là
	A. 1.	B. 0.	C. 2.	D. 4.
Câu 8: Phương trình nào sau đây vô nghiệm?
	A. 	 	B. 	
	C. 	D. 
Câu 9: Cho x thỏa mãn phương trình Giá trị lớn nhất tìm được của là
	A. 0. 	B. 	C. 	D. 1.
Câu 10: Số họ nghiệm của phương trình là
	A. 4.	B. 3.	C. 2.	D. 1.
Câu 11: Phương trình nào sau đây vô nghiệm?
	A. 	B. 
	C. 	D. 
Câu 12: Nghiệm âm lớn nhất của phương trình là
	A. 	B. 	C. 	D. 
Câu 13: Số nghiệm của phương trình thỏa mãn điều kiện là
	A. 1.	B. 0.	C. 3.	D. 2.
Câu 14: Trong các phương trình sau phương trình nào có nghiệm?
	A. 	B. 	
	C. 	D. 
Câu 15: Điều kiện để phương trình có nghiệm là
	A. 	B. Không có giá trị nào của m.	
	C. 	D. 
Câu 16: Phương trình có nghiệm là
	A. 	B. 	
	C. 	D. Vô nghiệm.
Câu 17: Nghiệm của phương trình thỏa mãn điều kiện là
	A. 	B. 	C. 	D. 
Câu 18: Từ phương trình ta tìm được có giá trị bằng
	A. 	B. 	C. 	D. 
Câu 19: Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?
	A. 1.	B. 2.	C. 3.	D. 4.
Câu 20: Giá trị của m để phương trình có nghiệm là
	A. Không có giá trị nào của m.	B. 
	C. 	D. Cả A, B, C đều sai.
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN
Dạng 1. Phương trình thuần nhất
1- C
2- A
3- B
4- B
5- D
6- D
7- C
8- C
9- B
10- C
11- D
12- B
13- A
14- A
15- A
16- B
17- D
18- B
19- A
20- B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Phương trình có nghĩa 
Ta có 
Câu 2.
Phương trình có nghĩa 
Ta có 
Vậy phương trình có nghiệm âm lớn nhất là với 
Câu 3.
Phương trình có nghĩa 
Ta có 
Câu 4.
Phương trình có nghĩa 
Ta có 
Theo bài ra 
Câu 5.
Phương trình có nghĩa 
Điều kiện để phương trình có nghiệm 
Vậy phương trình vô nghiệm khi 
Câu 6.
Phương trình có nghĩa 
Điều kiện để phương trình có nghiệm 
Câu 7.
Phương trình có nghĩa 
Ta có 
Câu 8.
Phương trình có nghĩa Ta có 
Vậy phương trình có nghiệm.
Câu 9. 
Phương trình có nghĩa 
Ta có 
Vì nên 
Câu 10.
Phương trình có nghĩa
Ta có 
Câu 11.
Phương trình có nghĩa
Để phương trình có nghiệm thì (vô lí).
Vậy phương trình vô nghiệm.
Câu 12.
Phương trình có nghĩa
Ta có 
Vì nên 
Vậy phương trình có 4 nghiệm thỏa mãn đề bài.
Câu 13.
Phương trình có nghĩa
Ta có 
Câu 14.
Phương trình có nghĩa 
Ta có 
Vậy phương trình có nghiệm dương nhỏ nhất là với 
Câu 15.
Phương trình có nghĩa 
Ta có 
Vậy phương trình có nghiệm dương nhỏ nhất là với 
Câu 16.
Phương trình có nghĩa 
Ta có 
Câu 17.
Phương trình có nghĩa 
Ta có 
Để phương trình (1) có nghiệm thì 
Câu 18.
Phương trình có nghĩa 
Ta có 
Giải (1) ta có 
Giải (2) ta có 
Câu 19.
Phương trình có nghĩa 
Ta có 
Câu 20.
Phương trình có nghĩa 
Ta có 
Trường hợp 1: 
Trường hợp 2: 
Dạng 2. Phương trình bậc hai của hàm số lượng giác
1- C
2- A
3- A
4- A
5- C
6- B
7- C
8- B
9- A
10- D
11- D
12- A
13- B
14- C
15- C
16- B
17- B
18- A
19- A
20- C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Phương trình có nghĩa 
Đặt Ta có (do).
Với ta có 
Câu 2.
Phương trình có nghĩa 
Đặt Ta có (do ).
Với ta có 
Câu 3.
Phương trình có nghĩa 
Đặt Ta có (do ).
Với ta có 
Vậy nghiệm dương bé nhất của phương trình là 
Câu 4.
Phương trình có nghĩa 
Đặt 
Ta có (do).
Với ta có 
Vì nên phương trình chỉ có 3 nghiệm.
Câu 5.
Phương trình có nghĩa 
Đặt Ta có 
Với ta có 
Với ta có 
Vì nên 
Câu 6.
Phương trình có nghĩa 
Đặt . Ta có 
Với ta có 
Câu 7.
Phương trình có nghĩa 
Đặt Ta có (do).
Với ta có 
Câu 8.
Phương trình có nghĩa 
Đặt Ta có (do).
Với ta có 
Câu 9.
Phương trình có nghĩa 
Đặt Ta có 
Với ta có 
Với ta có 
Câu 10.
Phương trình có nghĩa 
Ta có 
Đặt 
Ta có (do).
Với ta có 
Vậy nghiệm âm lớn nhất của phương trình là 
Câu 11.
Ta có (vô nghiệm).
Ta có (vô nghiệm).
Ta có nên phương trình (vô nghiệm)
Câu 12.
Phương trình có nghĩa Đặt 
Ta có (do).
Với ta có 
Vì nên phương trình có hai nghiệm.
Câu 13.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Với ta có 
Câu 14.
Phương trình có nghĩa 
Đặt Ta có 
Với ta có 
Với ta có 
Vì nên 
Vậy phương trình có 6 nghiệm thỏa mãn đề bài.
Câu 15.
Phương trình có nghĩa 
Đặt 
Ta có (do).
Vậy phương trình vô nghiệm.
Câu 16.
Phương trình có nghĩa 
Đặt Ta có 
Với ta có
Với ta có (vô nghiệm).
Vậy 
Câu 17.
Phương trình có nghĩa 
Ta có 
Vì thì (*) vô nghiệm nên 
Câu 18.
Phương trình có nghĩa 
Ta có 
Vì không là nghiệm của phương trình (1) nên ta chia cả hai vế của phương trình cho . 
Ta có 
Đặt Ta có 
Với ta có 
Với ta có 
Câu 19.
Ta có 
(Điều kiện ).
Đặt ta có 
Câu 20.
Phương trình có nghĩa 
Ta có 
Dạng 3. Phương trình lượng giác đẳng cấp
1- D
2- A
3- D
4- B
5- C
6- C
7- D
8- B
9- A
10- C
11- C
12- A
13- C
14- A
15- B
16- D
17- C
18- B
19- C
20- A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Phương trình có nghĩa 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta được
Câu 2.
Phương trình có nghĩa khi 
Chia cả 2 vế của phương trình cho ta được
Câu 3.
Phương trình có nghĩa 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta được
Câu 4.
Phương trình có nghĩa 
Ta có 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta được
Vậy giá trị nguyên của là 
Câu 5.
Phương trình có nghĩa 
Ta có 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta được
Câu 6.
Phương trình có nghĩa 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta được
Câu 7.
Phương trình có nghĩa 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta được
Câu 8.
Phương trình có nghĩa 
Ta có 
Câu 9.
Phương trình có nghĩa 
Ta có 
Có phương trình vô nghiệm.
Câu 10.
Phương trình có nghĩa 
Với 
Với (loại).
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta có
Vậy phương trình có 1 họ nghiệm.
Câu 11.
Phương trình có nghĩa 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta có
Kết hợp nghiệm ta được 
Câu 12.
Phương trình có nghĩa 
Ta có 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta có
 (vô nghiệm).
Câu 13.
Phương trình có nghĩa 
Ta có 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta có
Câu 14.
Phương trình có nghĩa 
Với phương trình vô nghiệm.
Với Chia cả hai vế của phương trình cho ta có
(Vô lí).
Vậy phương trình vô nghiệm.
Câu 15.
Phương trình có nghĩa 
Ta có 
Với Chia cả hai vế của phương trình cho ta có
Câu 16.
Phương trình có nghĩa 
Ta có 
Vì nên với 
Phương trình có 1 nghiệm thỏa mãn đề bài.
Câu 17.
Phương trình có nghĩa 
Ta có 
Vậy phương trình có 2 họ nghiệm.
Câu 18.
Phương trình có nghĩa 
Ta có 
 (1)
Với .
(loại).
Với Chia cả hai vế của phương trình cho ta có
Vậy 
Câu 19.
Phương trình có nghĩa 
Ta có 
Chia cả hai vế của phương trình (3) cho ta được
Do vô nghiệm nên 
Vậy phương trình có 1 họ nghiệm.
Câu 20.
Phương trình có nghĩa 
Với 
Ta có Để phương trình có nghiệm thì 
Với Chia cả hai vế của phương trình cho ta có
Để phương trình có nghiệm thì 
Dạng 4. Phương trình lượng giác đối xứng
1- C
2- D
3- A
4- C
5- A
6- B
7- B
8- D
9- B
10- B
11- A
12- C
13- D
14- C
15- D
16- B
17- A
18- B
19- C
20- B 
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Phương trình có nghĩa 
Đặt 
Ta có 
Câu 2.
Phương trình có nghĩa 
Ta có 
Đặt 
Ta có 
Do nên 
Với ta có 
Câu 3.
Phương trình có nghĩa 
Ta có 
Đặt 
Ta có 
Do nên 
Với ta có 
Câu 4.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Với ta có 
Vậy nghiệm dương nhỏ nhất của phương trình là 
Câu 5.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Do nên 
Với ta có 
Câu 6.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Câu 7.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
 (loại).
Vậy phương trình vô nghiệm hay không có nghiệm thỏa mãn 
Câu 8.
Phương trình có nghĩa 
Ta có 
Vậy phương trình vô nghiệm.
Câu 9.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Với ta có 
Với ta có 
Vậy giá trị lớn nhất của 
Câu 10.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Với ta có 
Với ta có 
Vậy phương trình có 3 họ nghiệm.
Câu 11.
Phương trình có nghĩa 
Ta có (1)
Đặt Ta có 
(loại).
Vậy phương trình vô nghiệm.
Câu 12.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Do nên 
Với ta có 
Vậy nghiệm âm lớn nhất của phương trình là 
Câu 13.
Phương trình có nghĩa 
Ta có 
Đặt Ta có 
Với ta có .
Do nên 
Vậy có 2 nghiệm thỏa mãn đề bài.
Câu 14.
Ta có Phương trình vô nghiệm.
Ta có Phương trình vô nghiệm.
Ta có Phương trình vô nghiệm.
Câu 15.
Phương trình có nghĩa 
Ta có 
Có 
Câu 16.
Phương trình có nghĩa 
Ta có 
Đặt 
Ta có 
Do nên 
Với ta có 
Câu 17.
Phương trình có nghĩa 
Ta có 
Đặt 
Ta có 
Do nên 
Với ta có 
Do nên 
Câu 18.
Phương trình có nghĩa 
Ta có 
Đặt 
Ta có 
Với ta có 
Câu 19.
Phương trình có nghĩa 
Đặt 
Ta có 
Do 
Để phương trình có nghiệm thì 
Vì nên 
Câu 20.
Phương trình có nghĩa 
Ta có . (1)
Đặt 
Ta có 
 Phương trình luôn có hai nghiệm phân biệt 
Theo Vi-ét ta có 
Suy ra luôn có ít nhất một nghiệm thỏa mãn .
Vậy phương trình luôn có nghiệm.