Giáo án Đại số Lớp 11 - Chủ đề: Định nghĩa và ý nghĩa đạo hàm (Tiết 1) - Vũ Thuỳ Linh

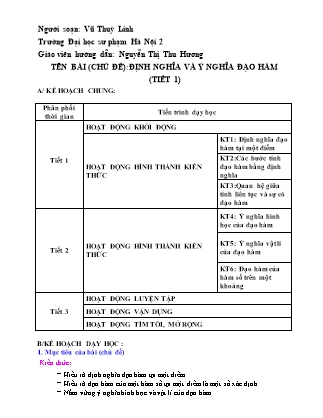
Người soạn: Vũ Thuỳ Linh
Trường Đại học sư phạm Hà Nội 2
Giáo viên hướng dẫn: Nguyễn Thị Thu Hương
TÊN BÀI (CHỦ ĐỀ):ĐỊNH NGHĨA VÀ Ý NGHĨA ĐẠO HÀM
(TIẾT 1)
A/ KẾ HOẠCH CHUNG:
Phân phối thời gian
Tiến trình dạy học
Tiết 1
HOẠT ĐỘNG KHỞI ĐỘNG
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
KT1: Định nghĩa đạo hàm tại một điểm 
KT2:Các bước tính đạo hàm bằng định nghĩa
KT3:Quan hệ giữa tính liên tục và sự có đạo hàm
Tiết 2
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
KT4: Ý nghĩa hình học của đạo hàm
KT5: Ý nghĩa vật lí của đạo hàm
KT6: Đạo hàm của hàm số trên một khoảng
Tiết 3
HOẠT ĐỘNG LUYỆN TẬP
HOẠT ĐỘNG VẬN DỤNG
HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG
B/KẾ HOẠCH DẠY HỌC:
I. Mục tiêu của bài (chủ đề)
 Kiến thức:
Hiểu rõ định nghĩa đạo hàm tại một điểm.
Hiểu rõ đạo hàm của một hàm số tại một điểm là một số xác định.
Nắm vững ý nghĩa hình học và vật lí của đạo hàm.
Hiểu rõ mối quan hệ giữa tính liên tục và sự tồn tại đạo hàm.
Kỹ năng: 
Biết cách tính đạo hàm tại một điểm bằng định nghĩa của các hàm số thường gặp.
Vận dụng tốt vào viết phương trình tiếp tuyến.
Thái độ:
Tư duy các vấn đề của toán học một cách lôgic và hệ thống.
Đinh hướng phát triển năng lực:
- Năng lực hợp tác: Tổ chức nhóm học sinh hợp tác thực hiện các hoạt động.
- Năng lực tự học, tự nghiên cứu: Học sinh tự giác tìm tòi, lĩnh hội kiến thức và phương pháp giải quyết bài tập và các tình huống.
- Năng lực giải quyết vấn đề: Học sinh biết cách huy động các kiến thức đã học để giải quyết các câu hỏi. Biết cách giải quyết các tình huống trong giờ học.
- Năng lực thuyết trình, báo cáo: Phát huy khả năng báo cáo trước tập thể, khả năng thuyết trình.
II. Chuẩn bị của giáo viên và học sinh
1. Giáo viên:
- Thiết kế hoạt động học tập hợp tác cho học sinh tương ứng với các nhiệm vụ cơ bản của bài học. 
- Tổ chức, hướng dẫn học sinh thảo luận, kết luận vấn đề.
2. Học sinh:
- Mỗi học sinh trả lời ý kiến riêng và phiếu học tập. Mỗi nhóm có phiếu trả lời kết luận của nhóm sau khi đã thảo luận và thống nhất.
- Mỗi cá nhân hiểu và trình bày được kết luận của nhóm bằng cách tự học hoặc nhờ bạn trong nhóm hướng dẫn.
- Mỗi người có trách nhiệm hướng dẫn lại cho bạn khi bạn có nhu cầu học tập.
III. Chuỗi các hoạt động học:
TIẾT 1.
GIỚI THIỆU (HOẠT ĐỘNG TIẾP CẬN BÀI HỌC) (10’)
* Mục tiêu: 
+ Tạo sự chú ý cho học sinh để vào bài mới.
+ Tạo tình huống để học sinh tiếp cận với khái niệm “đạo hàm”.
* Nội dung, phương thức tổ chức:
	+ Chuyển giao:
L1. Quan sát các hình ảnh (máy chiếu)
L2. Lớp chia thành các nhóm (nhóm có đủ các đối tượng học sinh, không chia theo lực học) và tìm câu trả lời cho các câu hỏi H1, H2, H3. Các nhóm viết câu trả lời vào bảng phụ.
H1. Theo em ở bức ảnh dưới đây chú công an giao thông đang làm gì?
H2. Vận tốc của vận động viên tại các thời điểm khác nhau có bằng nhau không? Có tính được vận tốc tại thời điểm cụ thể được không?
H3. Một dòng điện chạy trong dây dẫn. Tính thời gian và cường độ dòng điện chạy qua dây dẫn tại thời điểm t0 đến t? Tính cường độ trung bình của dòng điện? 
Hình 1
Hình 2
+ Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi H1, H2, H3. Viết kết quả vào bảng phụ.
+ Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi.
- HS quan sát các phương án trả lời của các nhóm bạn. 
- HS đặt câu hỏi cho các nhóm bạn để hiểu hơn về câu trả lời.
- GV quan sát, lắng nghe, ghi chép.
+ Đánh giá, nhận xét, tổng hợp:
 - GV nhận xét thái độ làm việc, phương án trả lời của các nhóm, ghi nhận và tuyên dương nhóm có câu trả lời tốt nhất. Động viên các nhóm còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo. 
- Dự kiến các câu trả lời:
TL1. Hình 1 chú công an đang bắn tốc độ các loại xe.
 TL2 Vận động viên trong hình 1 chạy trên quãng đường được tính theo công thức 
t
s
t1
_
_
+
++
M
N
S0
_
_
+
++
t0
_
_
+
++
S1
_
_
+
++
O
_
_
+
++
Giả sử tại thời điểm , vận động viên ở vị trí có ; tại thời điểm , vận động viên ở vị trí có . Khi đó, trong khoảng thời gian từ đến , quãng đường vận động viên chạy được là . Vậy vận tốc trung bình của vận động viên trong khoảng thời gian đó là (1)Nếu càng nhỏ thì tỉ số (1) càng phản ánh chính xác hơn sự nhanh chậm của VĐV tại thời điểm . Từ đó, người ta xem giới hạn của tỉ số khi dần đến là vận tốc tức thời tại thời điểm của VĐV, kí hiệu là 
Nói cách khác, .
Bài toán tìm vận tốc tức thời
Quãng đường s của chuyển động là một hàm số của thời gian t 	s = s(t)
Giới hạn hữu hạn (nếu có) đgl vận tốc tức thời của chuyển động tại thời điểm t0.
TL 3. Đ1. Thời gian: t – t0. Cường độ: Q(t) – Q(t0)
 Đ 2. Cường độ trung bình của dòng điện:	Itb = 
· GV dẫn dắt tương tự như bài toán tìm vận tốc tức thời.
Bài toán tìm cường độ tức thời
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t 	Q = Q(t)
Giới hạn hữu hạn (nếu có) đgl cường độ tức thời của dòng điện tại thời điểm t0.
* Sản phẩm: 
+ Các phương án giải quyết được ba câu hỏi đặt ra ban đầu.
+ Đưa ra được dự đoán: “Định nghĩa đạo hàm”.
- Tùy vào chất lượng câu trả lời của HS, GV có thể đặt vấn đề: Nhiều vấn đề của toán học, vật lí, hóa học, sinh học, ... dẫn đến bài toán tìm giới hạn:Trong toán học người ta gọi giới hạn trên là đạo hàm của hàm số tại điểm (nếu giới hạn này là hữu hạn). Đó chính là nội dung bài học “Định nghĩa và ý nghĩa đạo hàm”.
NỘI DUNG BÀI HỌC (HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC)
*Mục tiêu: Học sinh nắm được 4 đơn vị kiến thức của bài.
*Nội dung: Đưa ra các phần lý thuyết và có ví dụ ở mức độ NB, TH. 
*Kỹ thuật tổ chức: Thuyết trình, Tổ chức hoạt động nhóm.
*Sản phẩm: HS nắm được định lý, các hệ quả và giải các bài tập mức độ NB,TH.
I.Đạo hàm của hàm số tại một điểm: 
I.1. Định nghĩa đạo hàm của hàm số tại một điểm:
* Mục tiêu: 
	- Học sinh biết được khái niệm của hàm số liên tục tại một điểm.
	- Áp dụng để xét tính liên tục của một số hàm số tại một điểm cho trước.
 - Hình thành cách tính đạo hàm bằng định nghĩa.
* Nội dung, phương thức tổ chức:
Tiếp cận (khởi động)(10’)
Vận tốc tức thời
Cường độ dòng điện tức thời
Tốc độ phản ứng hóa học tức thời
ĐẠO HÀM
+ Chuyển giao:
	NV: * Học sinh đọc định nghĩa SGK. 
 * Học sinh giải quyết 2 hoạt động: HÐI.1.1; HÐI.1.2.
	 * Từ việc so sánh kết quả của 2 hoạt động, đưa ra cách tính đạo hàm 
 bằng định nghĩa ( dùng trực tiếp định nghĩa hoặc dùng ).
Hoạt động
Gợi ý
HÐI.1.1
Cho hàm số . Tính ?
HÐI.1.2
Đặt là số gia của đối số tại 
 : số gia tương ứng của hàm số. 
a.Tính ?
b.So sánh kết quả và 
c. Nêu các buớc tính đạo hàm bằng định nghĩa của hàm số ?
=
+ Thực hiện: Học sinh suy nghĩ và làm ví dụ vào giấy nháp.
 + Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác thảo luận để hoàn thiện lời giải.
 + Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa lời giải, từ đó nêu cách tính đạo hàm bằng định nghĩa và đạo hàm trên một khoảng. HS viết bài vào vở.
Hình thành kiến thức(5’)
Từ kết quả bài toán 1, ta suy ra cách tính đạo hàm bằng định nghĩa:
I.2. Các bước tính đạo hàm bằng Định nghĩa :
Bước 1: Giả sử là số gia của đối số tại , tính 
Bước 2: Lập tỉ số 
Bước 3: Tìm 
Củng cố(7’)
 Củng cố.
Gợi ý
Tính đạo hàm của các hàm số sau bằng định nghĩa
a) tại điểm x0 =1
b) tại x0 = 0
Gọi là số gia tại điểm x0 = 1, ta có:
 Suy ra: 
Vậy, y’(1) = 2.
b) Gọi là số gia tại điểm x0 = 0, ta có:
Suy ra: 
Vậy, y’(0) = -2.
I.3.QUAN HỆ GIỮA SỰ TỒN TẠI CỦA ĐẠO HÀM VÀ TÍNH LIÊN TỤC CỦA HÀM SỐ.
+ Mục tiêu: Học sinh biết được mối liên hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số
+ Nội dung, phương thức tổ chức:
a)Tiếp cận (khởi động)(5’)
+) HĐ1: Khởi động.
· Xét hàm số
H1. Tính ?
H2. Nếu hàm số gián đoạn tại thì nó có đạo hàm tại điểm đó không?
H3. Nếu một hàm số liên tục tại 1 điểm có thể khẳng định được hàm số đó có đạo hàm tại điểm đó hay không?
+ Chuyển giao:
	NV: * Học sinh đọc định nghĩa SGK. 
 * Học sinh giải quyết 3 câu hỏi:H1, H2, H3.
+ Thực hiện: Học sinh suy nghĩ và trả lời vào giấy nháp.
Đ1. 
Þ không tồn tại 
Đ 2. Þ không có f¢(0).
Đ 3. Nếu hàm số gián đoạn tại thì nó không có đạo hàm tại điểm đó. Nếu một hàm số liên tục tại 1 điểm chưa thể khẳng định được hàm số đó có đạo hàm tại điểm đó hay không.
 + Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác thảo luận để hoàn thiện lời giải.
 + Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa lời giải, từ đó nêu định lí về quan hệ giữa đạo hàm và liên tục. HS viết bài vào vở.
b)Hình thành kiến thức(3’)
Định lí. Nếu hàm số f(x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.
Chú ý:
a) Nếu y = f(x) gián đoạn tại x0 thì nó không có đạo hàm tại x0.
b) Nếu y = f(x) liên tục tại x0 thì có thể không có đạo hàm tại x0.
c) Củng cố:(5’)
+) HĐ3: Củng cố.
GỢI Ý
Ví dụ 1. Cho hàm số . Xét tính liên tục của hàm số đã cho, tính đạo hàm tại x=0.