Đề kiểm tra học kì I môn Toán 11 (số 4)

Đề kiểm tra học kì I (Số 4)
I. Phần trắc nghiệm (20 câu 6 điểm)
Câu 1: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là:
A. 	B. 	C. 	D. 
Câu 2: Phương trình vô nghiệm khi và chỉ khi:
A. 	B. 	C. 	D. 
Câu 3: Phương trình: có nghiệm là:
A. 	B. 	C. 	D. 
Câu 4: Phương trình có nghiệm là
A. .	 B. .	C. .	 D. .
Câu 5: Phương trình có nghiệm trên khi tất cả các giá trị thỏa mãn: A. .	B. .	C. .	D. .
Câu 6:	Cho phương trình: . Để phương trình có nghiệm thì giá trị thích hợp của tham số là A. .	 B. .	 C. .	 D. .
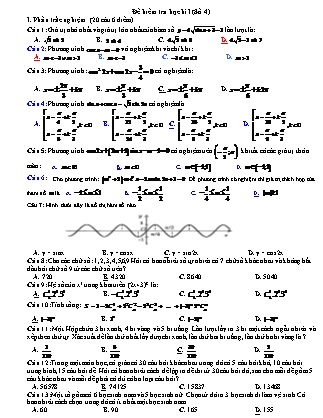
Câu 7: Hình dưới đây là đồ thị hàm số nào
 A. y = sinx B. y = cosx C. y = sin2x D. y = cos2x
Câu 8: Cho các chữ số: 1,2,3,4,5,6,9. Hỏi có bao nhiêu số tự nhiên có 7 chữ số khác nhau và không bắt đầu bởi chữ số 9 từ các chữ số trên?
 A. 720	B. 4320	C. 8640	D. 5040 
Câu 9: Hệ số của x5 trong khai triển (2x+3)8 là:
 A. 	B. 	C. 	D. 
Câu 10: Tính tổng: 
 A. 	 B. 	C. 	D. 
Câu 11: Một Hộp chứa 3 bi xanh, 4 bi vàng và 5 bi trắng. Lần lượt lấy ra 3 bi một cách ngẫu nhiên và xếp theo thứ tự. Xác suất để lần thứ nhất lấy được bi xanh, lần thứ hai bi trắng, lần thứ ba bi vàng là ?
 A. 	 B. 	 C. 	 D. 
Câu 12: Trong một môn học, cô giáo có 30 câu hỏi khác nhau trong đó có 5 câu hỏi khó, 10 câu hỏi trung bình, 15 câu hỏi dễ. Hỏi có bao nhiêu cách để lập ra đề thi từ 30 câu hỏi đó, sao cho mỗi đề gồm 5 câu khác nhau và mỗi đề phải có đủ cả ba loại câu hỏi?
 A. 56578	 B. 74125	C. 15837	D. 13468
Câu 13: Một tổ gồm có 6 học sinh nam và 5 học sinh nữ. Chọn từ đó ra 3 học sinh đi làm vệ sinh. Có bao nhiêu cách chọn trong đó có ít nhất một học sinh nam.
 A. 60	B. 90	C. 165	D. 155
Câu 14: Một hộp đựng các số tự nhiên có 4 chữ số được thành lập từ các chữ số 0,1,2,3,4 . Bốc ngẫu nhiên một số . Tính xác suất để số tự nhiên được bốc ra là số có 4 chữ số mà chữ số đằng trước nhỏ hơn chữ số đằng sau . A. 	 B. 	 C. 	 D.
Câu 15: Cho khai triển . Tìm , biết hệ số của số hạng thứ 3 bằng 5.	
 A. .	 B. .	 C. .	 D. .
B. 
Câu 16: Cho tam giác đều ABC như hình vẽ sau:
Phép quay nào trong các phép quay sau đây biến điểm B thành điểm C?
	A. Phép quay tâm C góc 600	 B. Phép quay tâm B góc 600	
	C. Phép quay tâm A góc -600 	 D. Phép quay tâm A góc 600	
Câu 17: Trong không gian, hai đường thẳng song song là:
	A. hai đường thẳng cùng nằm trên một mặt phẳng và không có điểm chung
 B. hai đường thẳng không cùng nằm trên một mặt phẳng 	 
 C. hai đường thẳng không có điểm chung D. hai đường thẳng cùng nằm trên một mặt phẳng 
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của BC. Mặt phẳng (α) đi qua M và song song mp(SAB). Gọi là thiết diện tạo bởi mp(α) và hình chóp S.ABCD. Tìm mệnh đề đúng?
A. là một lục giác .B. là một hình thang. C. là một tam giác. D. là một ngũ giác. 
Câu 19: Cho hình chóp S.ABCD có O là giao điểm của AC và BD, M là trung điểm của SD. Tìm giao điểm I của đường thẳng BM và mp(SAC).
	A. .	B. .	C. .	D. .
Câu 20: Cho hình hộp ABCD.A’B’C’D’ có M là trung điểm của A’D’. Tìm giao tuyến của hai mặt phẳng (ABM) và (A’B’C’D’).
	A. Đường thẳng Mx, với Mx song song với A’A’.B. Đường thẳng Mx, với Mx song song với A’B’.
	C. Đường thẳng Bx, với Bx song song với AM.D. Đường thẳng Bx, với Bx song song với AA’. 
Câu 21: Cho hình chóp S.ABCD, đáy là hình thang, đáy lớn AB, giao tuyến của mặt (SAD) và (SBC) là: A. SK với B. SK với C. SK với D. Sx với 
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD là đáy lớn. Mặt phẳng (α) chứa đường thẳng AB và cắt các cạnh SC, SD lần lượt tại các điểm phân biệt M, N . Tìm mệnh đề đúng? A. AD, CB và NM song song.	 B. AD, CB và NM đồng quy.
	 C. AB, CD và NM đồng quy.	D. AB, CD và NM song song.
Câu 23: Cho mặt phẳng (P) và đường thẳng d Ì (P). Mệnh đề nào sau đây đúng:
 A. Nếu A d thì A(P). B. Nếu A Î (P) thì A Î d.
 C. " A, A Î d Þ A Î (P).D. Nếu 3 điểm A, B, C Î (P) và A, B, C thẳng hàng thì A, B, C Î d.
II. Phần tự luận: (4 điểm)
Câu 1. Giải phương trình 2sin22x + sin2x – 3 = 0 (1 điểm)
Câu 2. Giao một đồng tiền 3 lần. Tính xác suất biến cố
A: “Để ba lần gieo đều xuất hiện mặt sắp” (0,5 điểm)
B: “Chỉ lần thứ hai xuất hiện mặt sắp” (1 điểm)
Câu 3. Cho hình chóp S.ABCD . Gọi M là một điểm nằm trong tam giác SCD
Tìm giao tuyến của hai mp (SBM) và (SAC) (1 điểm)
Tìm giao điểm của đường thẳng BM và mp (SAC) (0, 5 điểm)
Câu 1. Giải phương trình 2sin22x + sin2x – 3 = 0 (1 điểm)
Giải: 2sin22x + sin2x – 3 = 0 
 sin2x = 1 2x = x = 
Vậy phương trình đã cho có nghiệm x = 
Câu 2. Giao một đồng tiền 3 lần. Tính xác suất biến cố
A: “Để ba lần gieo đều xuất hiện mặt sắp” (0,5 điểm)
Giải. Số kết quả có thể là : {SSS; SSN;SNS;SNN; NNN; NNS; NSN; NSS}. n() = 8
 Số kết quả thuận lợi cho Alà : {SSS}. n(A) = 1
 Xác suất của biến cố A là P(A) = 
B: “Chỉ lần thứ hai xuất hiện mặt sắp” (1 điểm)
 Số kết quả thuận lợi cho B là: {NSN}. n(B) = 1
 Xác suất của biến cố B là P(B) = 
Câu 3. Cho hình chóp S.ABCD . Gọi M là một điểm nằm trong tam giác SCD
Tìm giao tuyến của hai mp (SBM) và (SAC) (1 điểm)
Tìm giao điểm của đường thẳng BM và mp (SAC) (0, 5 điểm)
Giải.
a) Tìm giao tuyến của hai mp (SBM) và (SAC)
Gọi N = SM CD Khi đó (SBM) chính là (SBN)
Như vậy (SBM) (SAC) cũng chính là (SBN) (SAC) 
Ta thấy S (SBN) (SAC) (1)
Gọi O = BN AC
 Suy ra O BN, BN (SBN) nên O (SBN)
 O AC, AC (SAC) nên O (SAC)
	Vậy O (SBN) (SAC) (2)
	Từ (1) và (2) cho ta (SBN) (SAC) = SO
 b) Tìm giao điểm của đường thẳng BM và mp (SAC)
 Trong (SBN) gọi I = BN SO
 Ta thấy I BN
 I SO, SO (SAC), nên O (SAC)
Vậy I = BM (SAC)